Array 1395 统计作战单位数

2020-11-24

n 名士兵站成一排。每个士兵都有一个 独一无二 的评分 rating 。

每 3 个士兵可以组成一个作战单位，分组规则如下：

从队伍中选出下标分别为 i、j、k 的 3 名士兵，他们的评分分别为 rating[i]、rating[j]、rating[k]
作战单位需满足： rating[i] < rating[j] < rating[k] 或者 rating[i] > rating[j] > rating[k] ，其中 0 <= i < j < k < n
请你返回按上述条件可以组建的作战单位数量。每个士兵都可以是多个作战单位的一部分。

1
2
3

输入：rating = [2,5,3,4,1]
输出：3
解释：我们可以组建三个作战单位 (2,3,4)、(5,4,1)、(5,3,1)

思路：这个问题可以转化为有一个数组 rating，数组元素不重复，按照下标的顺序找到顺序排序的 3 元组个数。

1 暴力破解法

先用两重 for 循环找到符合条件的 3 个数的前 2 个数
前 2 个数的排序情况分 2 种情况继续寻找第 3 个数
直接用 3 层循环，判断条件为 rating[i] < rating[j] && rating[j] < rating[k]) || (rating[i] > rating[j] && rating[j] > rating[k])

public int numTeams(int[] rating) {
 int n = rating.length;
 int ans = 0;
 for(int i = 0;i < n;i++){
     for(int j = i +1 ;j < n;j++){
        //  第二个数比第一个数大 继续找比第二数大的
        //  if(rating[j] > rating[i]){
        //      for(int k = j+1;k < n;k++){
        //          if(rating[k] > rating[j]) cnt++;
        //      }
        //  }else{
        //         for(int k = j+1;k < n;k++){
        //          if(rating[k] < rating[j]) cnt++;
        //      } 
        //  }
        if ((rating[i] < rating[j] && rating[j] < rating[k]) || (rating[i] > rating[j] && rating[j] > rating[k])) {
            ++ans;
         }

     }
 }
 return cnt;   
}

时间复杂度：$O(n^3)$

空间复杂度：O(1)

3 层 for 循环，减少代码量.

2 枚举中间点

枚举三元组(i,j,k)中的 j，之后统计：

出现在位置 j 左侧且比 j 评分低的士兵数量 $i_$
出现在位置 j 左侧且比 j 评分高的士兵数量 $i_$
出现在位置 j 右侧且比 j 评分低的士兵数量 $k_$
出现在位置 j 右侧且比 j 评分高的士兵数量 $k_$

这样 $i_,i,k_$ 组成的3个数是依次递增的； $i_, k，k_ $ 组成的 3 个数就是递减的。因此以 j 为中间点的三元组的个数为：
$$
i_k_ + i_k_
$$

for(int j = 1;j < n-1;++j){
  int iless= 0,imore = 0,kless=0,kmore=0; 
    //  j 左边的数
    for(int i = 0;i < j;++i){
        if(rating[i] > rating[j]) ++imore;
        else ++iless;
    }
   //  j 右边的数
   for(int k = j+1;k < n;++k){
        if(rating[k] > rating[j]) ++kmore;
        else ++kless;
   }
    // 累加
   cnt += iless*kmore + imore*kless ;
}
 return cnt ;

时间复杂度：双重 for 循环

空间复杂度：除了答案，不需要额外的存储空间

3

树状数组

树状数组就是用数组来模拟树形结构，可以解决大部分基于区间上的更新已经求和问题。线段树的结构如下：

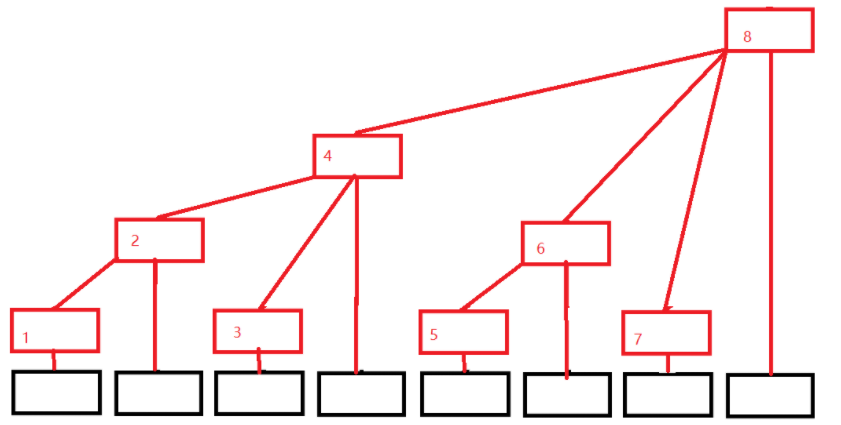
黑色数组代表原来的数组（下面用A[i]代替），红色结构代表我们的树状数组(下面用C[i]代替)，发现没有，每个位置只有一个方框，令每个位置存的就是子节点的值的和，则有

$C[i] = A[i - 2k+1] + A [i - 2k+2] + … + A[i]$; k为i的二进制中从最低位到高位连续零的长度。例如i = 8(1000)时候，k = 3。

求和：$SUM_i = C[i] + C[i-2^{k1}] + C[(i - 2^{k1}) - 2^{k2}] + …..；$

lowbit ：$2^k = i&(-i)$，lowbit 的值就是$2^k $

建立树状数组

求和功能

根据上面的求和公式

更新功能

更新某个A[i]的值，则会影响到所有包含有A[i]位置，则$C[i + 2^k]、C[(i + 2^k) + 2^k]…$ 都会受到影响。

求 lowbit 值的功能

int n;
int a[1005],c[1005]; //对应原数组和树状数组

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){    //在i位置加上k
    while(i <= n){
        c[i] += k;
        i += lowbit(i);
    }
}

int getsum(int i){        //求A[1 - i]的和
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

树状数组的优点和缺点

修改和查询的复杂度都是O(logN)，而且相比线段树（就是二叉树）系数要少很多，比传统数组要快，而且容易写。

缺点是遇到复杂的区间问题还是不能解决，功能还是有限。

int n = rating.length;

maxN = n + 2;

c = new int[maxN];

disc = new ArrayList(); disc.add(rating[i]); disc.add(-1);//通过 rating 数组建立一个树状数组，disc 的数值是树状数组

Collections.sort(disc); //排序

int id = getId(rating[i]);

https://www.cnblogs.com/xenny/p/9739600.html