强化学习 Sarsa

2020-08-21

Sarsa

Sarsa 的决策部分和 Q learning 一样，都是基于 Q 表的形式决策, 在 Q 表中挑选值较大的动作值施加在环境中来换取奖惩.。但是不同的地方在于 Sarsa 的更新方式是不一样的。

Q learning 估算动作，但并不一定会执行这个动作，Q-learning 在这一步只是估计了一下接下来的动作值。而sarsa 估算的动作也是接下来要做的动作。因为 Sarsa 是说到做到型, 所以我们也叫他 on-policy, 在线学习, 学着自己在做的事情。在 sarsa 算法中，行动策略和目标策略都是epsilon-greedy。相比之下q-learning只有行动策略是epsilon-greedy，而目标策略是贪婪策略。

算法的区别：

action_ 不同：Sarsa 在当前 state 已经想好了 state 对应的 action, 而且想好了下一个 state_ 和下一个 action_ ，在下一个 state 就会执行这个action_，Qlearning 还没有想好下一个 action_，这里只是估计了 action_，会在下一个 state 里面重新选择 action。
Sarsa 更新 Q(s,a) 的时候基于的是下一个 Q(s_, a_) ，Qlearning 是基于 maxQ(s_)，因为此时 q_learing 还没有确定下一步的 action_

这样看来 Q learning 每次都是朝着 maxQ(s_) 去选择 actions ，他看起来更加勇敢也变得贪婪。Sarsa 是尽量避免踩坑，在陷阱周围，agent 看起来更加犹豫，它是一种保守的算法, 他在乎每一步决策,。

算法的代码形式

开始初始化 observation ，在当前状态下选择一个 action
通过与环境交互然后获得下一个 observation_ ，reward ,
估算下一个action_,
开始学习，更新 q 表
把当前状态下确定的 observation_ 和 action_ 交换为下一个状态的 observation 和 action
在下一个状态直接执行这个action_,获得接下来的 observation_。

update 的代码如下

def update():
    for episode in range(50):

        # 1. initial observation
        observation = env.reset()
        # 2. RL choose action based on observation
        action = RL.choose_action(str(observation))
        while True:

            # 3. fresh env
            env.render()

            # 4. RL tack action and get next obseration and reward and done
            observation_, reward, done = env.step(action)

            # 5. RL choose action based on next observation
            action_ = RL.choose_action(str(observation_))

            # 6. RL learn from thie transition
            RL.learn(str(observation), action, reward,
                     str(observation_), action_)

            # 7. swap observation and action
            observation = observation_
            action = action_

            if done:
                break

    # end of game
    print('game over')
    env.destory()

学习 learn， Q 值是根据 q(s, a) 来确定的

def learn(self, s, a, r, s_, a_):
    self.check_state_exist(s_)
    # 预测值
    q_predict = self.q_table.loc[s, a]
    if s_ != 'terminal':
        # 真实值
        q_target = r + self.gamma * self.q_table.loc[s_, a_]  # update
    else:
        # 真实值
        q_target = r
    # 更新 Q 表
    self.q_table.loc[s, a] += self.lrate * (q_target - q_predict)

Sarsa(lambda)

Sarsa 是一种单步更新，也就是每走一步就会更新一次,并记录这些 state(但是并没有记录这些 state 距离宝藏的是更近更快还是更慢)，在一开始因为对最优值没有头绪，会在原地打转重复，最后才会找到最优值，这些重复打转看起来就很没有必要，反而影响效率。那怎么让 Sarsa 也知道哪些步数是距离最优解近的，哪些是远的，从而更新距离宝藏近的步数？

单步更新 and 回合更新

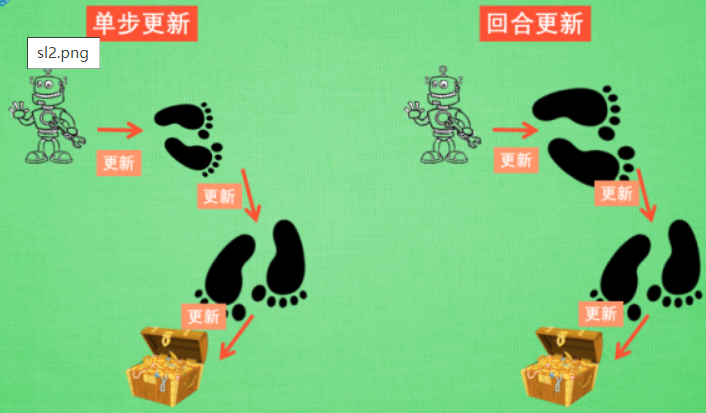
单步更新是每一步都会进行更新 Q表，但是在没有获取宝藏的时候, 我们现在站着的这一步也没有得到任何更新（这一步是离宝藏近还是离宝藏远无从知道）, 直到获取宝藏时, 我们才为获取到宝藏的上一步更新为: 这一步很好, 和获取宝藏是有关联的, 而之前为了获取宝藏所走的所有步都被认为和获取宝藏没关系。

回合更新是等到这回合结束, 才开始对本回合所经历的所有步都添加更新, 但是这所有的步都是和宝藏有关系的, 都是为了得到宝藏需要学习的步, 所以每一个脚印在下回合被选则的几率又高了一些.，在这种角度来看, 回合更新似乎会有效率一些。

Sarsa($\lambda$)

为了让 Sarsa 知道哪一步离宝藏近，需要引入一个参数 lambda 。其实 lambda 就是一个衰变值, 他可以让你知道离奖励越远的步可能并不是让你最快拿到奖励的步, 所以我们想象我们站在宝藏的位置, 回头看看我们走过的寻宝之路, 离宝藏越近的脚印越看得清, 远处的脚印太渺小, 我们都很难看清, 那我们就索性记下离宝藏越近的脚印越重要, 越需要被好好的更新. 和之前我们提到过的奖励衰减值 gamma 一样, lambda 是脚步衰减值, 都是一个在 0 和 1 之间的数.

当 lambda 取0, 就变成了 Sarsa 的单步更新, 当 lambda 取 1, 就变成了回合更新, 对所有步更新的力度都是一样. 当 lambda 在 0 和 1 之间, 取值越大, 离宝藏越近的步更新力度越大. 这样我们就不用受限于单步更新的每次只能更新最近的一步, 我们可以更有效率的更新所有相关步了

Sarsa-lambda 算法

算法如下：E(s,a) 是一个用来记录 lambda 的表格，它和 Q table 结构相同。$\delta$ 是误差： $q_{现实} - q_{预测}$。更新 Q table 和 E table 的公式是：
$$
Q(s, a) = Q(s, a) + α [R + {\gamma} Q(s_, a_) - Q(s, a)]E(s, a)\
\

E(s, a) = \gamma\lambda E(s, a)
$$

学习 learn

Sarsa-lambda 的一开始创建了结构和 Q table 相似的 eligibility_trace 表。表格的横轴是 state，纵轴是 action，value 值是 lambda 的衰减值（也就是记录了每个走过的 action 距离最优解的是否更近更快），解决了 Sarsa 单步更新只会更新到达最优解的 action。

eligibility_trace

初始化时，浅拷贝 Q table： self.eligibility_trace = self.q_table.copy()
和 q_table 一样 check_state_exist ，加入新的 state 到表中，默认值为全 0
更新 Q table 的时候: 公式按照上面的公式来。
更新 eligibility_trace ：对于经历过的 state-action, 我们让他+1, 证明他是得到 reward 路途中不可或缺的一环。
- 每经过的 [ s,a] value 值都 +1 ，但是考虑累加值，每次都让 [s,:]所在的行所有值重置为 0 ，之后在 [ s,a] +1。
- lambda 衰减。定义一个衰减系数 $\lambda$,每次eligibility_trace 的值都乘以一个$\lambda$ (衰减系数)和 γ (对未来奖励衰减系数)


def learn(self, s, a, r, s_, a_):
    self.check_state_exist(s_)
    q_predict = self.q_table.loc[s, a]
    if s_ != 'terminal':
        q_target = r + self.gamma * self.q_table.loc[s_, a_]
    else:
        q_target = r
    error = q_target - q_predict

    # 这里开始不同
    # 对于经历过的 state-action, 我们让他+1, 证明他是得到 reward 路途中不可或缺的一环

    # Method 2:
    self.eligibility_trace.loc[s, :] *= 0
    self.eligibility_trace.loc[s, a] = 1

    # Q table update
    self.q_table += self.lrate * error * self.eligibility_trace

    # decay eligibility trace after update
    self.eligibility_trace *= self.gamma*self.lambda_