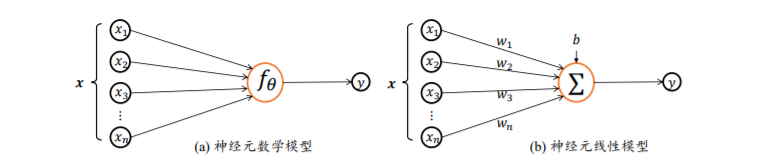
神经元数学模型
神经元输 入向量𝒙 = [𝑥1, 𝑥2, 𝑥3, … , 𝑥𝑛 ] T,经过函数映射:𝑓𝜃: 𝒙 → 𝑦后得到输出𝑦,其中𝜃为函数𝑓自 身的参数。考虑一种简化的情况,即线性变换:𝑓(𝒙) = 𝒘T𝒙 + 𝑏,展开为标量形式: 𝑓(𝒙) = 𝑤1𝑥1 + 𝑤2𝑥2 + 𝑤3𝑥3 + ⋯ + 𝑤𝑛𝑥𝑛 + b
参数𝜃 = {𝑤1, 𝑤2, 𝑤3, . . . , 𝑤𝑛, 𝑏}确定了神经元的状态,通过固定𝜃参数即可确定此神经元 的处理逻辑。
简化神经网络只有一个输入,𝑦 = 𝑤𝑥 + 𝑏 。其中𝑤参数可以理解为直线的斜率(Slope),b 参数为 直线的偏置(Bias)。此时只需要两个观测值,就可以求解出 w 和 b。当采样多个数据的时候,可能不存在一条直 线完美的穿过所有采样点。退而求其次,我们希望能找到一条比较“好”的位于采样点中 间的直线
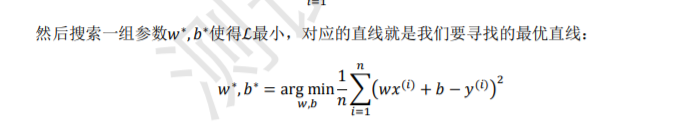
梯度下降算法,它通过循环计算函数的梯度∇𝑓并 更新待优化参数𝜃,从而得到函数𝑓获得极小值时参数𝜃的最优数值解。
对于预测值是连续的实数范围,或者属于某一段连续的实数区间,我们把这种问题称为回归(Regression)问题。特别地,如果 使用线性模型去逼近真实模型,那么我们把这一类方法叫做线性回归(Linear Regression, 简称 LR),有离散值预测问题成为分类问题。
线性回归
首先假设 𝑛 个输入的生物神经元的数学模型为线性模 型之后,只采样𝑛 + 1个数据点就可以估计线性模型的参数𝒘和𝑏。引入观测误差后,通过 梯度下降算法,我们可以采样多组数据点循环优化得到𝒘和𝑏的数值解。
神经网络原理理解
https://www.jianshu.com/p/e112012a4b2d
神经网络有输入层、隐藏层和输出层。每层都有很多神经元。
输入层就是负责接收信息,比如说一只猫的图片。输出层就是计算机对这个输入信息的认知,它是不是猫。隐藏层就是对输入信息的加工处理。
训练神经网络,输入大量的数据。每个神经元都有属于它的激活函数,用这些函数给计算机一个刺激行为。第一次输入图片之后,有部分的神经元被激活,被激活的神经元所传递的信息是对输出结果最有价值的信息。如果输出的结果被判定为是狗,也就是说是错误的了,那么就会修改神经元,一些容易被激活的神经元会变得迟钝,另外一些神经元会变得敏感。这样一次次的训练下去,所有神经元的参数都在被改变,它们变得对真正重要的信息更为敏感。
搭建神经网络基本流程:
定义添加神经层的函数
- Weights
- biases
- Wx_plus_b —》 outputs = activation_function(Wx_plus_b)
训练数据 :x_data ,noise ,y_data 真实数据
定义节点准备接受数据 :define placeholder for inputs to network x,y
定义神经层:隐藏层和预测层, ,预测层的结果就是输出值
定义loss表达式:ys 和 输出值之间的差别
选择 optimer 使loss达到最小,optimer 优化 bias 和 weight ,反过来更新神经元。
Tensorflow
在输入层输入数据,然后数据飞到隐藏层飞到输出层,用梯度下降处理,梯度下降会对几个参数进行更新和完善,更新后的参数再次跑到隐藏层去学习,这样一直循环直到结果收敛。
过程就是:建图->启动图->运行取值
问题:
用梯度下降处理数据,什么时候梯度下降更新和完善参数
激励函数在预测层,判断哪些值要被送到预测结果那里 ??