leetcode 04 寻找两个正序数组的中位数

2020-07-09

给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出这两个正序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。你可以假设 nums1 和 nums2 不会同时为空。

示例 1:

1
2
3

nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0

示例 2:

1
2
3

nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5

已知：两个数组都是按照顺序存储的，通过数组长度可以知道中位数是数组中的某 1 个元素，还是 2 个元素的平均值。

思路：定义一个数组，将数组1 和数组 2 中的元素按照顺序存储，这样问题就转化成求顺序排列元素的中位数。

合并数组 1 和数组 2 分为 3 种情况：

数组1的所有元素都小于数组2 中的元素，这样只需把数组 2 合并到数组 1上面
数组2 的所有元素都小于数组1 中的元素，这样只需把数组 1 合并到数组 2上面
其他情况，就通过遍历数组 1 和 2 每个元素进行比较，依次存入数组

遇到的问题

确定中位数的位置：（n1 + n2) / 2

因为 js 的两数相除可以是小数，用 parseInt（）方法会分两种情况（整除和不整除），向上取整，这样 Math.ceil((n1 + n2) / 2) - 1 就是中位数的下标或者第一个下标（两个数）。

怎么合并两个数组

1	nums1.push.apply(nums1, nums2)// 第一个参数是将 nums2 里面元素的 this 指向 nusm1

要考虑合并数组的第 3 中情况，可能会存在一个数组遍历完，另一个数组还存在数据，所以还需要进行判断
假设两个有序数组的长度分别为 m 和 n，时间复杂度(m+n)，空间复杂度是 O(m+n)O(m+n)。

我的暴力解法

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
        var findMedianSortedArrays = function(nums1, nums2) {
            const arr = []
            const n1 = nums1.length,
                n2 = nums2.length

            //  flag 为 0 表示中位数是两个数组元素的平均数，为 1 表示是数组元素
            const flag = (n1 + n2) % 2 == 0 ? 0 : 1
                // 中位数在arr 数组中的位置是midn 或者 是midn 和 midn+1 的平均数
            const midn = Math.ceil((n1 + n2) / 2) - 1

            // 数组1 所有元素小于 数组2
            if (nums1[n1 - 1] <= nums2[0]) {
                nums1.push.apply(nums1, nums2)
                return flag == 0 ? (nums1[midn] + nums1[midn + 1]) / 2 : nums1[midn]
                    //  数组2 所有元素小于 数组1
            } else if (nums2[n2 - 1] <= nums1[0]) {
                nums2.push.apply(nums2, nums1)
                return flag == 0 ? (nums2[midn] + nums2[midn + 1]) / 2 : nums2[midn]
            }

            let i = 0,
                j = 0;
            while (i < n1 && j < n2) {
                if (nums1[i] <= nums2[j]) {
                    arr.push(nums1[i])
                    i++
                } else {
                    arr.push(nums2[j])
                    j++
                }
                // if(i = n1)
            }
            // 数组1中还存在元素
            while (i < n1) {
                arr.push(nums1[i])
                i++
            }
            // 数组2中还存在元素
            while (j < n2) {
                arr.push(nums2[j])
                j++
            }
            return flag == 0 ? (arr[midn] + arr[midn + 1]) / 2 : arr[midn]
        };

官方解法

官方介绍了一种二分查找法

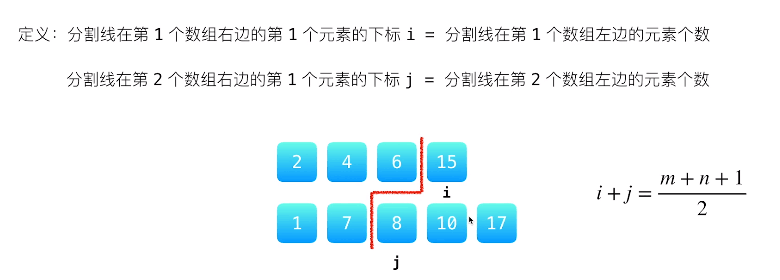
建立了如下模型，这个模型中位数必然和分割线两侧的 4 个数据有关，这样找中位数问题就转化为求分界线两侧的最值问题或者左侧的最值问题。

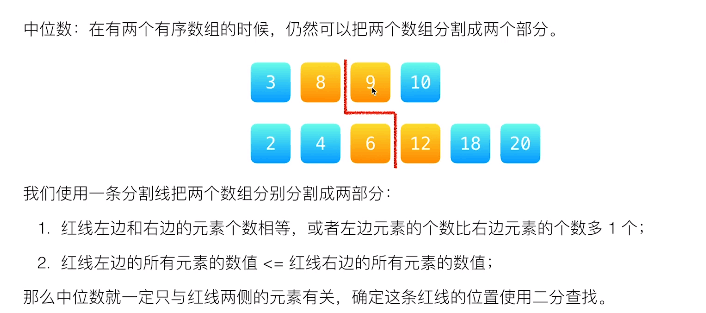
分析模型

第一种情况：两个数组长度之和是奇数，假设中位数在左侧，让左侧元素比右侧元素多一个

第二种：两个数组之和都是偶数，左侧和右侧元素一样多

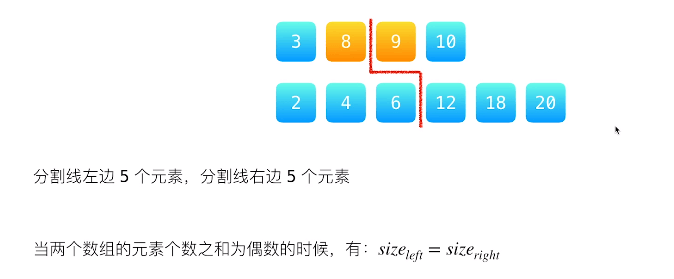
从这个模型中我们可以获取什么

假设数组 1 的长度是 m，假设数组2 的长度是 n。

当 m + n 为偶数的时候，$size_ = \frac{m+n}{2}= \frac{m+n+1}{2}$

当 m + n 为偶数的时候就是上面的第一种情况，左边多一位，$size_ = \frac{m+n}{2}= \frac{m+n+1}{2}$

可以得出结论这个模型，$size_ = \frac{m+n}{2}= \frac{m+n+1}{2}$，$size_$ 就是 m+n-$size_$

如何建立这个模型呢？

从上图可以看出这个模型：分割线左边的元素 <= 红线右边的所有元素数值。我们需要把普通的模型转化为这个标砖模型。

1.第一行的数组记为 num1（数组长度较短），第二类的数组记为 num2（数组长度较长），之后在异常情况说明为什么要把数组长度较短放在第一行。

2.num1 和 num2 元素中间画一条分割线（奇数左边多分一个元素）

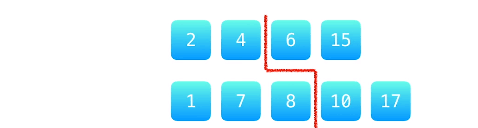
3.比较分割线左右的 4 个数字，只要不符合 分割线左边的元素 <= 红线右边的所有元素数值 关系，就调整 num1 和 num2 的分界线。

分割线移动的准则是：

1
2
3

+ num1 分割线左侧第一个数 <= num2 分割线右侧第一个数
+ num1 分割线右侧第一个数 >= num2 分割线左侧第一个数
只要不满足上面的取反条件，就需要移动分割线

以上面这个为例：num2 分割线的左侧 8 比 num1分割线右侧的 6大，此时 num1 的分割线应该右移，num2 的分割线响应左移（满足分割线两边数组均分问题）。修改之后的如下图，满足模型的规律，而且我们很轻易发现中无数就是分割线左侧的最大值 7 。

极端问题的讨论

1）分割线在 num1 的最多边，或者最右边

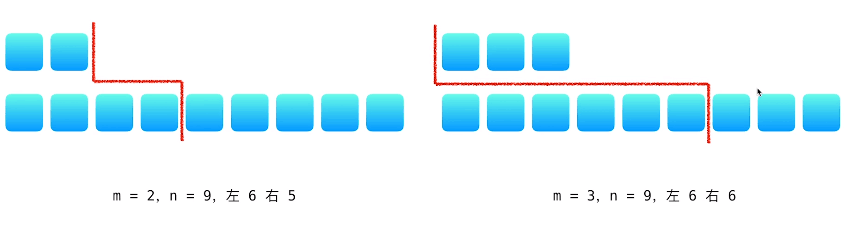
我们需要访问 “中间数分割线”左右两边的元素，因此需要在需要在较短的数组上确定“中间分隔线”的位置。数组长度较短的放在 num1的位置

2）两数组元素相等，分割线在两数组的头尾，这种情况也依然可以用上面的模型解决。

建立模型

1.将数组较短的替换为 num1

2.计算分割线的元素个数 totalLeft = (m + n + 1) / 2

3.以 num1 的下标不会越界作为循环条件，根据 nums2[j-1] <= nums1[i] 取反进行修改分割线。[left ,i,right] 进行二分法查找。

i 是num1 分割线右侧第一个数，i = left + (right + left) / 2
j 是num2 分割线右侧第一个数 j = totalLeft - i
果 nums2[j - 1] > nums1[i],则 num2 左侧的数据大于 num1 右侧数据（num1右侧数据小了，num2左侧数据大了），此时应该 num1 的分割线右移，num2 分割线左移。也说明此时 num1 分割线左侧的数据不需要筛选二分区间变为 [left,i + 1]

如果 nums2[j - 1] <= nums1[i],则 num2 左侧数据小于 num1右侧数据满足一边条件，还需要判断，num1左侧数据是否小于 num2 右侧数据，因此num1的分割线左移，num2的分割线右移。一直到 left == right。
跳出循环的时候 left 取值是 num1 右侧的第一个数

4.讨论中位数

模型完成之后，我们需要讨论 nums1LeftMax 、nums1RgihtMin、nums2LeftMax、nums2RightMin这4个数值

分割线在 num1 的最左侧，说明 num1所有的数都大于 num2 分割线左侧的数，nums1LeftMax 是一个无效值
分割线在 num1 的最右侧，说明 num1所有的数都小于 num2 分割线右侧的数，nums1RgihtMin 是一个无效值
分割线在 num2 的最左侧，说明 num2 所有的数都大于 num1 分割线左侧的数，nums2LeftMax是一个无效值
分割线在 num2 的最右侧，说明 num2 所有的数都小于 num1 分割线有右的数，nums2RightMin是一个无效值

5.中位数求取

处理无效值之后，如果数组总长度是奇数，那么中位数 num1 和 num2 左侧的最大值。如果总长度是偶数，那么中位数是左侧最大数和右侧最大数的平均数。

代码如下

// 第一个数组个数是最少的
if (nums1.length > nums2.length) {
    [nums1, nums2] = [nums2, nums1]
}

const m = nums1.length
const n = nums2.length

// 分割线左边的所有元素需要满足的个数是 (m + n + 1) / 2
const totalLeft = Math.floor((m + n + 1) / 2);

// 在第一个数组的区间 [0,m] 里查找恰当的分割线
// 是的 num1[i-1] <= nums2[j] && nums2[j-1] <= nums1[i]
//  i 是第一个数组分割线右边的第一个元素下标 ， j 是第二个数组分割线右边的第一个元素下标
let left = 0,
    right = m

while (left <= right) //为了保证 num1 数组下标不会越界
{
    const i = left + Math.floor((right - left) / 2)
    const j = totalLeft - i
    const nums1LeftMax = i === 0 ? -Infinity : nums1[i - 1]
    const nums1RgihtMin = i === m ? Infinity : nums1[i]
    const nums2LeftMax = j === 0 ? -Infinity : nums2[j - 1]
    const nums2RightMin = j === n ? Infinity : nums2[j]
        // if (nums2[j - 1] > nums1[i]) {
        //     left = i + 1 // num2 左侧的数据 大于 num1 右侧数据（num1右侧数据小了，num2左侧数据大了），此时应该 num1 的分割线右移 ，num2 分割线左移
        //         // 也说明此时 num1 分割线左侧的数据不需要筛选 二分区间变为 [left,i + 1]
        // } else {

    //     right = i // num2 左侧数据 小于 num1右侧数据 满足一边条件，还需要判断，num1左侧数据是否 小于 num2 右侧数据，因此num1的分割线左移，num2的分割线右移
    //         // 下一轮搜索的区间 [left,i]
    // }
    if (nums1LeftMax <= nums2RightMin && nums1RgihtMin >= nums2LeftMax) { //nums1 左侧的数据小于 num2 右侧的数据 num1 右侧的值 大于num2 左侧的数据
        return (m + n) % 2 === 1 ?
            Math.max(nums1LeftMax, nums2LeftMax) :
            (Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RgihtMin, nums2RightMin)) / 2
    } else if (nums1LeftMax > nums2RightMin) { // num1 左侧数据 大于 num2右侧数据 分割线左移
        right = i - 1
    } else {
        left = left + 1 // num1 右侧数据 小于 num2左侧数据 分割线右移
    }
}